I’ve been thinking about the extent to which there is tension between the principles of Universal Design for Learning and progressive, inquiry-based, student-centered math teaching.
I’ve done a lot of math teaching in independent schools that falls within the rightmost section, and some in the sweet spot in the middle. Within the public and charter school system, the challenge has been more about moving from the splash of inaccessible, traditional math teaching into universally designed (but still fairly traditional) teaching.
For a bit of background, UDL is an educational framework that began in 1984 which calls for multiple means of engagement, representation, and action/expression to ensure access for all learners by removing barriers to learning. You may have seen this visual metaphor:


UDL is a rightfully ambitious framework which in practice is aspirational rather than fully realized in any particular lesson, unit, or course. When it comes to access to mathematics, the challenge is in the implementation details of any curriculum or pedagogical approach.
When I think about implementations of a progressive math teaching philosophy, approaches such as Exeter Math (problem sets) and Building Thinking Classrooms come to mind. I’ve used aspects of both of these over the years. Both of them hold student collaboration as a central course goal. They are both opinionated about how students should work (together, often at the board) and that students should learn by solving problems and generalizing from there.
I’ve been wondering lately about the extent to which these progressive, inquiry-based math approaches can be inaccessible to some students based on their learning needs. And if so, are these barriers that can be removed, or are they intrinsic to the particular approach?

I happen to be a huge fan of Exeter math. I love the spiraled problem sets, the fact that students are expected to own the cognitive lift, and the way the curriculum emphasizes connection, sense-making, and novel problem solving. At the same time, I also recognize that it’s not an approach that could be widely adopted at schools across the country. There are practical barriers in terms of the time commitment required outside of class, lack of board space and large class size in many places, and limited opportunities for differentiation. This makes me wonder about what a universally designed, problem-based approach would look like.
To meet the requirements of UDL, it seems the things we can be opinionated about as teachers and curriculum designers have to be limited. For example, we can still insist that students do most of the talking and thinking within the classroom. But we probably have to let get the requirement that students work in groups most of the time since this infringes on student choice. (To me, there is a balancing act to navigate between UDL Checkpoint 8.3 about collaboration and community and UDL Checkpoint 7.1 about individual choice and autonomy.) That’s a painful concession for me to consider because of how strongly I believe in the value of collaboration in math class.
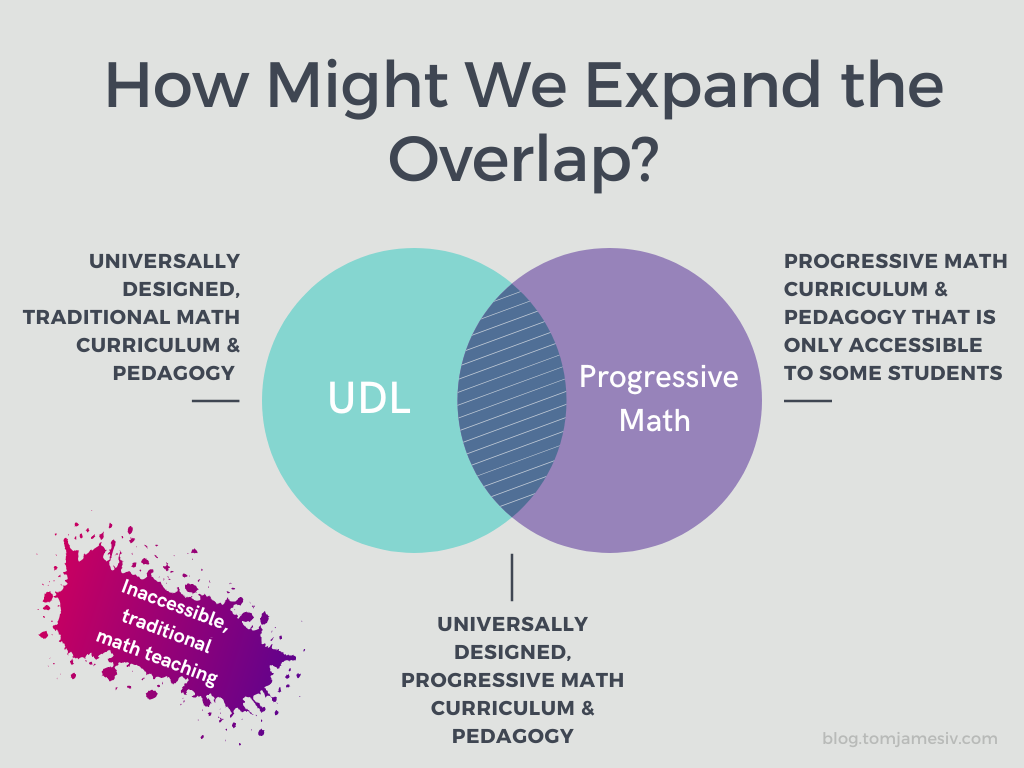
Expanding the Overlap
I’m sure many educators have found ways over the years to take these progressive math approaches and make them accessible to as many students as possible. I wonder if these are some of the both/and beliefs they embody:
- Student collaboration is a central course goal, and we provide choice for how students collaborate.
- Maybe the only option isn’t just students working together at the board or at their tables, but also in writing using Google Docs, post-its, etc.
- Novel problem-solving is required, and we provide literacy scaffolds, concept organizers, on-ramps, explicit instruction about strategy, and student choice of difficulty level
- Math is treated as a way to have fun with your brain in the same way that puzzles are fun, and direct applications and connections to students’ lives are regular features of our curriculum
- We keep the complexity of the math we ask students to learn, and provide multiple representations beyond text to support decoding and sense-making
- This might mean we need to step our visual design game!