Category / educational philosophy

by Tom James

Understanding Pushback on Inquiry-Based Math Learning

I teach in a progressive math department committed to inquiry-based learning, and I’ve been working on sharpening how I talk about why I believe in this approach.

A conversation will often start when I hear a student or a parent say one of these:

  • “I learn better with a traditional approach where we learn something and then practice it a bunch.”
  • “My kid needs a teacher who actually teaches.”
  • “I get that some students can figure out how to do math without being told how, but my kid just needs you to show them the steps to follow.”
  • “My teacher made us figure most of the material out on our own last year, which was frustrating. Instead of telling us the answer, they would just ask us more questions!”

It’s hard to imagine what an inquiry-based math class looks like if you’ve never been in one. I suspect that if you’re a parent and your child is experiencing math-related stress or frustration, there are a few reasons you might order if this way of learning is best for your child. These are some of the images you might conjure up:

  • Students working on a hard problem they’ve never seen before as the teacher watches silently from the side of the classroom
  • Students “learning” an incorrect approach and leaving the class with serious misconceptions
  • A teacher who de-emphasizes procedural fluency to the point that students while students can explain a concept or idea in broad strokes, they can’t actually solve any math problems
  • Students who are stuck, frustrated, and angry

When I think about an inquiry-based math class looks like, I see something very different:

  • Students engaged in problem-solving requiring them to notice patterns and wonder why they occur
  • Students having rich conversations with one another about math under the guidance of a thoughtful, attentive teacher
  • Students working hard to satisfy their own curiosity while being simultaneously “egged on” and supported by a caring teacher

Ultimately, every parent comes to these conversations about math education with the goal of seeing their child successful and happy. Keeping this in mind is critical for addressing their concerns.

Over at the IBL Blog, Stan Yoshinobu writes about the feelings can arise when students haven’t bought into the value of productive struggle:

Mindsets are at the core causes student buy-in issues. When students don’t buy it, it’s often because they don’t like being stuck or that being stuck implies there is something wrong with the problem, them, or the teacher or all of the above and more.

I was digging more into the IBL Blog and discovered this lovely metaphor of “I don’t learn this way” as the tip of the iceberg:

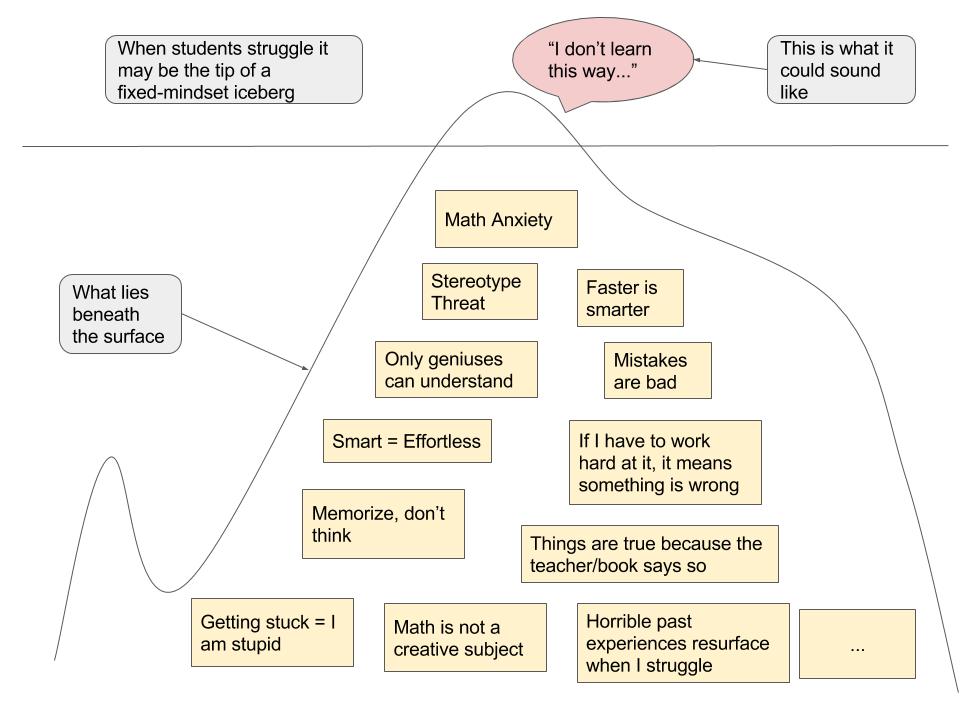
Iceberg 1

This imagery reminds us to look beneath the surface to find the source of resistance to inquiry-based learning. Only then can I speak to my beliefs and vision for my students.

I believe in inquiry-based learning because I think students learn math best when…

  • … they have a chance to explore ideas on their own before being told what the “best” strategy is for solving a problem.
  • … their mathematical ideas are affirmed and valued, even when they’re not fully clarified or correct yet.
  • … they are given opportunities to develop intuition before technical vocabulary and formalism are introduced.
  • … they are invited (and expected) to look for patterns and are regularly asked, “What do you notice?”
  • … teachers explicitly and implicitly communicate to students that mathematical knowledge is not isolated to select “experts” (like math teachers) who then dispense it to others, but rather that mathematical creativity is broadly accessible.
  • … they are invited (and expected) to pose questions of their own and are regularly asked, “What do you wonder?”
  • … teachers explicitly and implicitly communicate to students that the teacher’s mathematical questions are not the only interesting ones, but rather that the ability to ask a rich, thought-provoking question about math is broadly accessible.
  • … they see their peers employ a variety of successful strategies to solve a problem and are encouraged to understand multiple approaches.
  • … they are given opportunities to communicate their understanding to their classmates and receive guidance on how to improve their oral and written communication.
  • … there are structures to support collaboration with their peers.
  • … they spend most of their time in the sweet spot of productive struggle.
  • … they are given opportunities to apply the fruits of their intellectual labor during focused practice, building mastery and supporting long-term retention.

I’ll conclude with some prose from Joshua Bowman, who recently shared a preface he wrote to an IBL course. Here’s an excerpt:

… [T]he success of the class will depend on the pursuit of both individual excellence and collective achievement. Like a musician in an orchestra, you should bring your best work and be prepared to blend it with others’ contributions.

… Mistakes are inevitable, and they should not be an obstacle to further progress. It’s normal to struggle and be confused as you work through new material. Accepting that means you can keep working even while feeling stuck, until you overcome and reach even greater accomplishments.

by Tom James

Math is Like a Pomegranate

This is my contribution to The Virtual Conference of Mathematical Flavors.

“Math is like a pomegranate—intimidating, and kinda scary looking at first, but also incredibly fascinating and vibrant.”

In order to figure out what flavor of math I’ve been serving up in my classrooms over the past six years, I’m going to take a stab at Sam Shah’s idea of working backwards from what students have written about their experiences in my math classes. (Spoiler alert: the answer is apparently pomegranate; who knew?!) Of course, not all of my students have had transformative experiences and others have straight up had a bad time. But right now, I’m going to focus on the students who have been positively impacted in order to articulate what the best implementation of my ideals has felt like.

But to be honest, it feels way scarier to share the positive things students have written about me over the years than anything critical. When I was younger, I used to brag and show off; I thought that if people knew about all the things I was good at, they would have to like me. Once I figured out that this is not how relationships work, the pendulum swung hard in the other direction for me. I grew increasingly uncomfortable accepting compliments and I minimized my achievements, working to avoid even the appearance of self-promotion. It’s an ongoing struggle to get right-sized, but lately I’ve begun to internalize the idea that being excessively diminutive is its own barrier to connection.

So with that confession out in the open, here are some of my favorite reflections students have written. (The title of this post comes from one of these!)

A few years ago, I started asking students to write advice to next year’s students. And when I remember, I make sure to share this advice once the new group arrives. Here are some examples of what my students have written.

Reading these, some of the core beliefs I bring to my teaching are apparent to students in different courses and at different schools. I hope that my students internalize them as well:

  • Math is something to get excited about. I want my math-skeptical students stay curious about why certain people openly love math, and I want them to find reasons of their own for loving math. I’m not shy about telling them when I get goosebumps when talking about math, and I don’t hesitate to make corny memes—and be super proud of them—to show how highly I think of a mathematical idea or how much their understanding has grown. (See the “extending the definition of sine and cosine” trigonometry meme I made this year.)
  • Math is a playground for creativity. You can ask and answer your own questions. There are games to make up and play, connections to establish, new approaches and representations to develop, and structures to create and explore. Some of my favorite moments come when a student (or even better, a group of students) comes up with a solution pathway I’ve never considered or notices a pattern I’ve never seen before.
  • Engaging with math is an opportunity to build confidence. No matter where you are in your mathematical journey, there are ideas to wrestle with in math that are hard, but not impossible. It’s like an infinite gym for your brain with an endless selection of workouts. Realizing that you can do something you’d previously found scary, intimidating, or intractable is incredibly empowering.
  • Expect and welcome obstacles. In math, there’s nothing wrong with being wrong, and getting stumped is an invitation to push your thinking deeper or to try something else. For this reason, I react like it’s the most normal thing in the world when a student tells me their approach didn’t work or when they don’t know what to do next. Sometimes they get a little peeved when I don’t rescue them right away, and that’s okay!
  • Math is especially enjoyable when shared with others in a caring and trusting community. Despite the cultural trope of the solitary mathematical genius, there is no rule saying that math has to be a solo sport. The process of guiding another person to a mathematical idea you’ve uncovered requires patience, clear thinking, and careful consideration of what the other person is comprehending. Similarly, the practice of asking for and receiving guidance requires humility, self-awareness, and careful articulation of what you’re understanding and where you’re feeling fuzzy. To help with this, I treat the word obvious like a cuss word in math class, and students usually buy in pretty quickly!

As a final thought, it feels liberating to put this out there in a less formal way than I’ve articulated aspects of my educational philosophy in the past. For comparison, this is what I’ve used in previous job searches, and almost all of it was composed in 2014, before any of the student reflections above were written.

I still stand by everything in this document, but I really appreciate the type of unencumbered sharing Sam’s framing of the prompt for this virtual conference has facilitated. In other words, asking “What mathematical flavor are your serving up?” rather than “What’s your theory of mathematics education?” seems more likely to inspire folks to share a healthy multiplicity of approaches instead of competing formal philosophies. And, it gives us an opportunity to celebrate our wins instead of worrying about all of the things we’re not doing.