Category / inquiry-based learning

by Tom James

Expanding the Overlap: UDL and Progressive Math Pedagogy

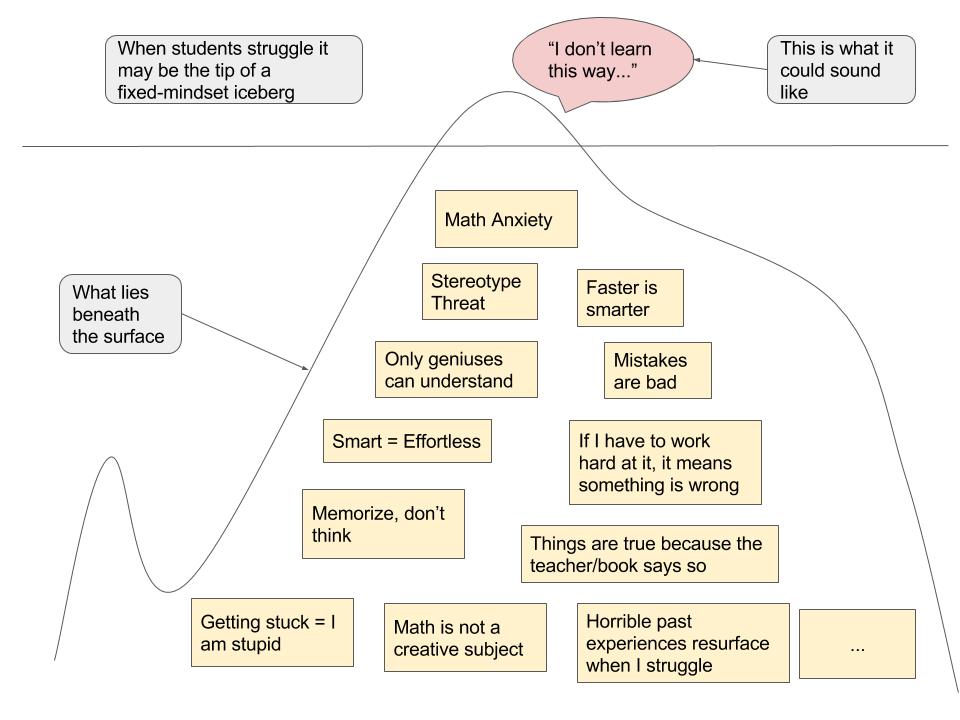
I’ve been thinking about the extent to which there is tension between the principles of Universal Design for Learning and progressive, inquiry-based, student-centered math teaching.

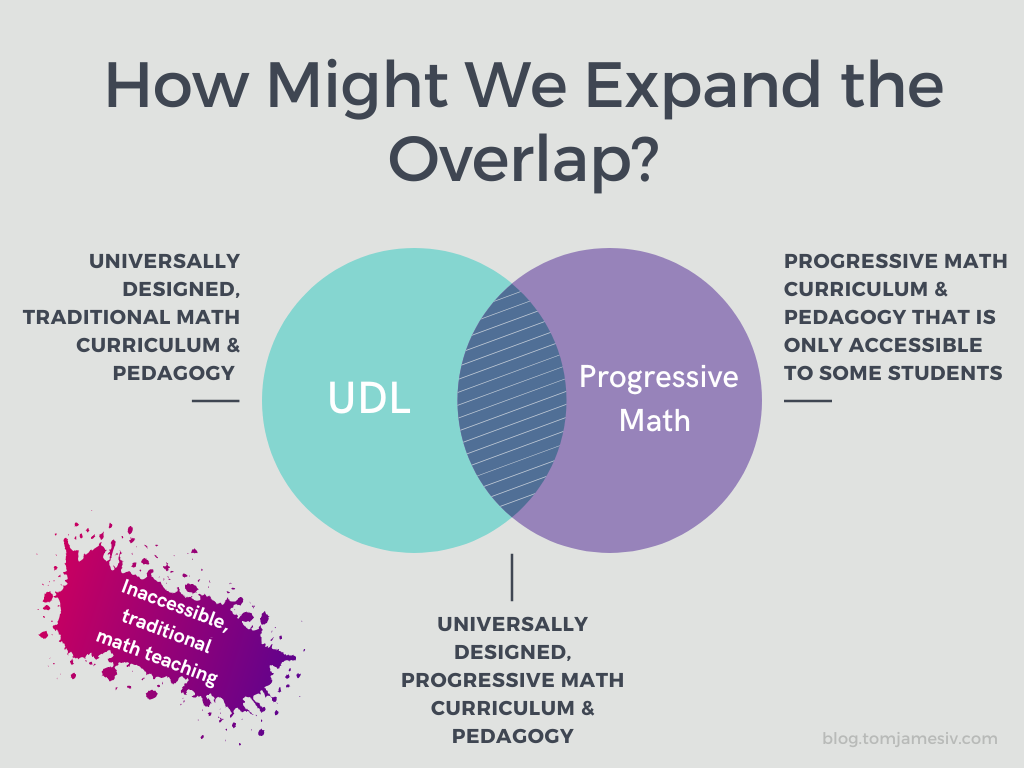
I’ve done a lot of math teaching in independent schools that falls within the rightmost section, and some in the sweet spot in the middle. Within the public and charter school system, the challenge has been more about moving from the splash of inaccessible, traditional math teaching into universally designed (but still fairly traditional) teaching.

For a bit of background, UDL is an educational framework that began in 1984 which calls for multiple means of engagement, representation, and action/expression to ensure access for all learners by removing barriers to learning. You may have seen this visual metaphor:

Here are the specific UDL guidelines:

UDL is a rightfully ambitious framework which in practice is aspirational rather than fully realized in any particular lesson, unit, or course. When it comes to access to mathematics, the challenge is in the implementation details of any curriculum or pedagogical approach.

When I think about implementations of a progressive math teaching philosophy, approaches such as Exeter Math (problem sets) and Building Thinking Classrooms come to mind. I’ve used aspects of both of these over the years. Both of them hold student collaboration as a central course goal. They are both opinionated about how students should work (together, often at the board) and that students should learn by solving problems and generalizing from there.

I’ve been wondering lately about the extent to which these progressive, inquiry-based math approaches can be inaccessible to some students based on their learning needs. And if so, are these barriers that can be removed, or are they intrinsic to the particular approach?

I happen to be a huge fan of Exeter math. I love the spiraled problem sets, the fact that students are expected to own the cognitive lift, and the way the curriculum emphasizes connection, sense-making, and novel problem solving. At the same time, I also recognize that it’s not an approach that could be widely adopted at schools across the country. There are practical barriers in terms of the time commitment required outside of class, lack of board space and large class size in many places, and limited opportunities for differentiation. This makes me wonder about what a universally designed, problem-based approach would look like.

To meet the requirements of UDL, it seems the things we can be opinionated about as teachers and curriculum designers have to be limited. For example, we can still insist that students do most of the talking and thinking within the classroom. But we probably have to let get the requirement that students work in groups most of the time since this infringes on student choice. (To me, there is a balancing act to navigate between UDL Checkpoint 8.3 about collaboration and community and UDL Checkpoint 7.1 about individual choice and autonomy.) That’s a painful concession for me to consider because of how strongly I believe in the value of collaboration in math class.

Expanding the Overlap

I’m sure many educators have found ways over the years to take these progressive math approaches and make them accessible to as many students as possible. I wonder if these are some of the both/and beliefs they embody:

  • Student collaboration is a central course goal, and we provide choice for how students collaborate.
    • Maybe the only option isn’t just students working together at the board or at their tables, but also in writing using Google Docs, post-its, etc.
  • Novel problem-solving is required, and we provide literacy scaffolds, concept organizers, on-ramps, explicit instruction about strategy, and student choice of difficulty level
  • Math is treated as a way to have fun with your brain in the same way that puzzles are fun, and direct applications and connections to students’ lives are regular features of our curriculum
  • We keep the complexity of the math we ask students to learn, and provide multiple representations beyond text to support decoding and sense-making
    • This might mean we need to step our visual design game!
by Tom James

Understanding Pushback on Inquiry-Based Math Learning

I teach in a progressive math department committed to inquiry-based learning, and I’ve been working on sharpening how I talk about why I believe in this approach.

A conversation will often start when I hear a student or a parent say one of these:

  • “I learn better with a traditional approach where we learn something and then practice it a bunch.”
  • “My kid needs a teacher who actually teaches.”
  • “I get that some students can figure out how to do math without being told how, but my kid just needs you to show them the steps to follow.”
  • “My teacher made us figure most of the material out on our own last year, which was frustrating. Instead of telling us the answer, they would just ask us more questions!”

It’s hard to imagine what an inquiry-based math class looks like if you’ve never been in one. I suspect that if you’re a parent and your child is experiencing math-related stress or frustration, there are a few reasons you might order if this way of learning is best for your child. These are some of the images you might conjure up:

  • Students working on a hard problem they’ve never seen before as the teacher watches silently from the side of the classroom
  • Students “learning” an incorrect approach and leaving the class with serious misconceptions
  • A teacher who de-emphasizes procedural fluency to the point that students while students can explain a concept or idea in broad strokes, they can’t actually solve any math problems
  • Students who are stuck, frustrated, and angry

When I think about an inquiry-based math class looks like, I see something very different:

  • Students engaged in problem-solving requiring them to notice patterns and wonder why they occur
  • Students having rich conversations with one another about math under the guidance of a thoughtful, attentive teacher
  • Students working hard to satisfy their own curiosity while being simultaneously “egged on” and supported by a caring teacher

Ultimately, every parent comes to these conversations about math education with the goal of seeing their child successful and happy. Keeping this in mind is critical for addressing their concerns.

Over at the IBL Blog, Stan Yoshinobu writes about the feelings can arise when students haven’t bought into the value of productive struggle:

Mindsets are at the core causes student buy-in issues. When students don’t buy it, it’s often because they don’t like being stuck or that being stuck implies there is something wrong with the problem, them, or the teacher or all of the above and more.

I was digging more into the IBL Blog and discovered this lovely metaphor of “I don’t learn this way” as the tip of the iceberg:

Iceberg 1

This imagery reminds us to look beneath the surface to find the source of resistance to inquiry-based learning. Only then can I speak to my beliefs and vision for my students.

I believe in inquiry-based learning because I think students learn math best when…

  • … they have a chance to explore ideas on their own before being told what the “best” strategy is for solving a problem.
  • … their mathematical ideas are affirmed and valued, even when they’re not fully clarified or correct yet.
  • … they are given opportunities to develop intuition before technical vocabulary and formalism are introduced.
  • … they are invited (and expected) to look for patterns and are regularly asked, “What do you notice?”
  • … teachers explicitly and implicitly communicate to students that mathematical knowledge is not isolated to select “experts” (like math teachers) who then dispense it to others, but rather that mathematical creativity is broadly accessible.
  • … they are invited (and expected) to pose questions of their own and are regularly asked, “What do you wonder?”
  • … teachers explicitly and implicitly communicate to students that the teacher’s mathematical questions are not the only interesting ones, but rather that the ability to ask a rich, thought-provoking question about math is broadly accessible.
  • … they see their peers employ a variety of successful strategies to solve a problem and are encouraged to understand multiple approaches.
  • … they are given opportunities to communicate their understanding to their classmates and receive guidance on how to improve their oral and written communication.
  • … there are structures to support collaboration with their peers.
  • … they spend most of their time in the sweet spot of productive struggle.
  • … they are given opportunities to apply the fruits of their intellectual labor during focused practice, building mastery and supporting long-term retention.

I’ll conclude with some prose from Joshua Bowman, who recently shared a preface he wrote to an IBL course. Here’s an excerpt:

… [T]he success of the class will depend on the pursuit of both individual excellence and collective achievement. Like a musician in an orchestra, you should bring your best work and be prepared to blend it with others’ contributions.

… Mistakes are inevitable, and they should not be an obstacle to further progress. It’s normal to struggle and be confused as you work through new material. Accepting that means you can keep working even while feeling stuck, until you overcome and reach even greater accomplishments.

by Tom James

Interesting Numbers v2

This is a follow-up post to my first day math problem from last year.

I’ve only posted once in a while over the past few years, but I’m very glad I spent the time last year to write about how my first day math problem went. After re-reading my post from last year, I was able to rapidly load the problem and how it went back into my memory, and I decided to make some of the changes I had written about.

Here’s the updated version of the problem, which adds scaffolding and will hopefully keep groups moving along who aren’t as comfortable with this type of open-ended exploration.

And here’s the checklist I’m going to use to keep myself organized as I walk around and monitor each group’s progress. (This idea comes from 5 Practices for Orchestrating Productive Mathematics Discussions by by Margaret S. Smith and  Mary Kay Stein.)

Feel free to pass along any feedback or take this a step further!

Resources: