I teach in a progressive math department committed to inquiry-based learning, and I’ve been working on sharpening how I talk about why I believe in this approach.
A conversation will often start when I hear a student or a parent say one of these:
- “I learn better with a traditional approach where we learn something and then practice it a bunch.”
- “My kid needs a teacher who actually teaches.”
- “I get that some students can figure out how to do math without being told how, but my kid just needs you to show them the steps to follow.”
- “My teacher made us figure most of the material out on our own last year, which was frustrating. Instead of telling us the answer, they would just ask us more questions!”
It’s hard to imagine what an inquiry-based math class looks like if you’ve never been in one. I suspect that if you’re a parent and your child is experiencing math-related stress or frustration, there are a few reasons you might order if this way of learning is best for your child. These are some of the images you might conjure up:
- Students working on a hard problem they’ve never seen before as the teacher watches silently from the side of the classroom
- Students “learning” an incorrect approach and leaving the class with serious misconceptions
- A teacher who de-emphasizes procedural fluency to the point that students while students can explain a concept or idea in broad strokes, they can’t actually solve any math problems
- Students who are stuck, frustrated, and angry
When I think about an inquiry-based math class looks like, I see something very different:
- Students engaged in problem-solving requiring them to notice patterns and wonder why they occur
- Students having rich conversations with one another about math under the guidance of a thoughtful, attentive teacher
- Students working hard to satisfy their own curiosity while being simultaneously “egged on” and supported by a caring teacher
Ultimately, every parent comes to these conversations about math education with the goal of seeing their child successful and happy. Keeping this in mind is critical for addressing their concerns.
Over at the IBL Blog, Stan Yoshinobu writes about the feelings can arise when students haven’t bought into the value of productive struggle:
Mindsets are at the core causes student buy-in issues. When students don’t buy it, it’s often because they don’t like being stuck or that being stuck implies there is something wrong with the problem, them, or the teacher or all of the above and more.
I was digging more into the IBL Blog and discovered this lovely metaphor of “I don’t learn this way” as the tip of the iceberg:
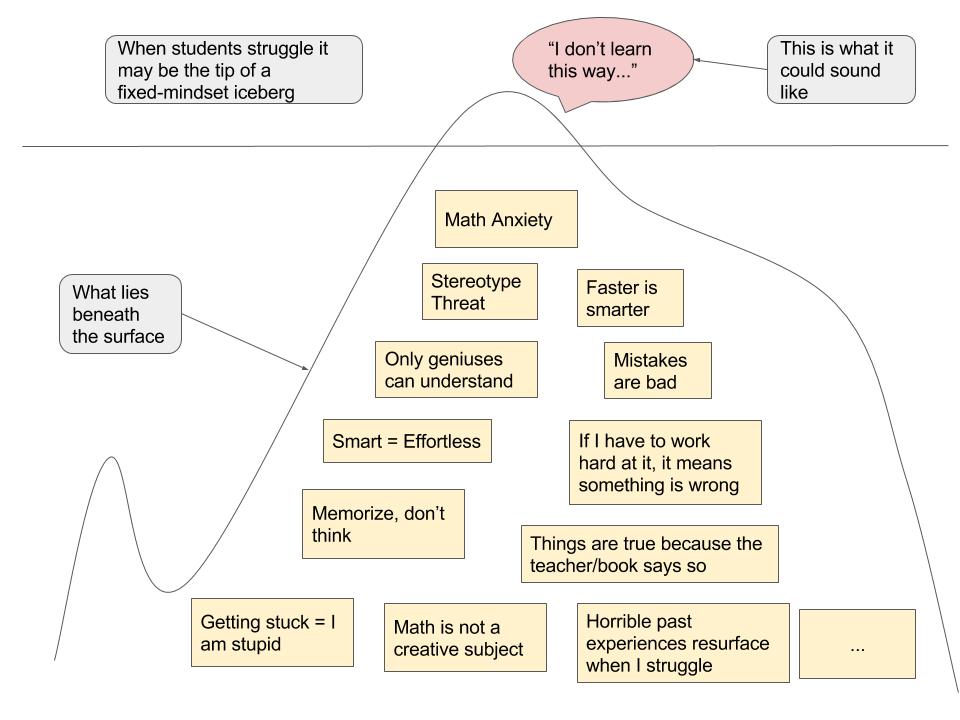
This imagery reminds us to look beneath the surface to find the source of resistance to inquiry-based learning. Only then can I speak to my beliefs and vision for my students.
I believe in inquiry-based learning because I think students learn math best when…
- … they have a chance to explore ideas on their own before being told what the “best” strategy is for solving a problem.
- … their mathematical ideas are affirmed and valued, even when they’re not fully clarified or correct yet.
- … they are given opportunities to develop intuition before technical vocabulary and formalism are introduced.
- … they are invited (and expected) to look for patterns and are regularly asked, “What do you notice?”
- … teachers explicitly and implicitly communicate to students that mathematical knowledge is not isolated to select “experts” (like math teachers) who then dispense it to others, but rather that mathematical creativity is broadly accessible.
- … they are invited (and expected) to pose questions of their own and are regularly asked, “What do you wonder?”
- … teachers explicitly and implicitly communicate to students that the teacher’s mathematical questions are not the only interesting ones, but rather that the ability to ask a rich, thought-provoking question about math is broadly accessible.
- … they see their peers employ a variety of successful strategies to solve a problem and are encouraged to understand multiple approaches.
- … they are given opportunities to communicate their understanding to their classmates and receive guidance on how to improve their oral and written communication.
- … there are structures to support collaboration with their peers.
- … they spend most of their time in the sweet spot of productive struggle.
- … they are given opportunities to apply the fruits of their intellectual labor during focused practice, building mastery and supporting long-term retention.
I’ll conclude with some prose from Joshua Bowman, who recently shared a preface he wrote to an IBL course. Here’s an excerpt:
… [T]he success of the class will depend on the pursuit of both individual excellence and collective achievement. Like a musician in an orchestra, you should bring your best work and be prepared to blend it with others’ contributions.
… Mistakes are inevitable, and they should not be an obstacle to further progress. It’s normal to struggle and be confused as you work through new material. Accepting that means you can keep working even while feeling stuck, until you overcome and reach even greater accomplishments.


