I decided to re-sequence my start-of-the-year activities and to lead with a low-floor, high-ceiling problem in assigned random groups of three or four students.
Here is the problem, which comes from Phillips Exeter Academy’s Math 1 curriculum:
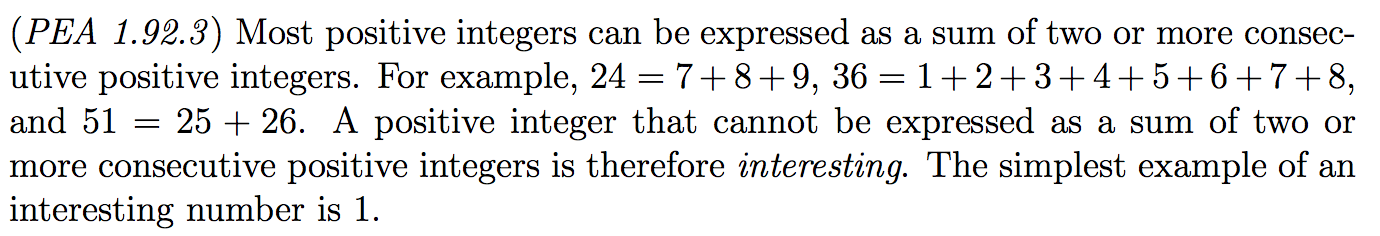
I told the groups to figure out everything they could about this situation with prompts like, “What do you notice about interesting numbers? What do you wonder about them?”
As I watched twelve groups of students explore this problem over three classes, I began to see students latch onto different aspects of this problem. All of these questions and discoveries are inter-related, so I’m writing them down now so that I can map them out in the future.
Questions:
- Which numbers up through 20 (or so) are interesting?
- Why are powers of 2 interesting?
- Are powers of 2 the only interesting numbers?
- Are there any interesting odd numbers?
- What happens when I sum any two consecutive positive integers?
- What happens when I sum any three consecutive positive integers?
- If n is odd, what happens when I sum any n consecutive positive integers?
- If n is even, what happens when I sum any n consecutive positive integers?
- How can I decompose any odd number?
- How can I decompose any multiple of 3?
- If n is odd, how can I decompose any multiple of n?
- How can I decompose any even number?
- Is there a general algorithm for decomposing any number?
- How many ways are there to decompose a given number?
Realizations:
- All powers of 2 are interesting.
- Only powers of 2 are interesting.
- No odd numbers are interesting.
- The sum of two consecutive positive integers is odd.
- The sum of three consecutive positive integers is a multiple of 3.
- If n is odd, the sum of n consecutive positive integers is a multiple of n.
- If n is even, the sum of n consecutive positive integers is n/2 more than a multiple of n.
- There is an algorithm for decomposing even numbers.
- There is exactly one way to decompose a prime number greater than 2.
- The powers of 2 are exactly the whole numbers without odd factors.
There was a split between groups that started by trying to answer (the very natural) question #1 (and thus getting to realizations #1 and #2) and those that started by generating and then trying to answer questions #5 and 6 (and thus getting to realizations #4 and #5). There was also one group in one class that decided to explore the sum of the first n consecutive integers (i.e., they wanted to know about the triangular numbers).
I think I will definitely use this problem again, with perhaps a bit more structure and guided mini-explorations along the way as groups arrive at various questions and realizations. It would probably be worth making a checklist for each group to help keep me organized as I keep tabs on each group’s progress.
Related: