Category / backwards design

by Tom James

Launch Problems for Optimization Unit

I’ve had the pleasure of teaching standard-level calculus with Sam Shah this school year, and recently we’ve been working with the students on optimization. Rather than starting with the canonical calculus optimization problems, we decided to jump in with maximizing the area of various shapes under curves:

Feb-01-2018 16-37-59.gif

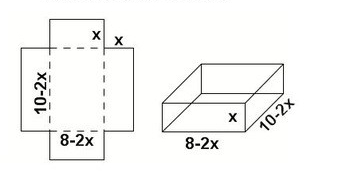
I think I first saw a problem like this in a textbook called Advanced Mathematics by Richard G. Brown (page 167, #12):

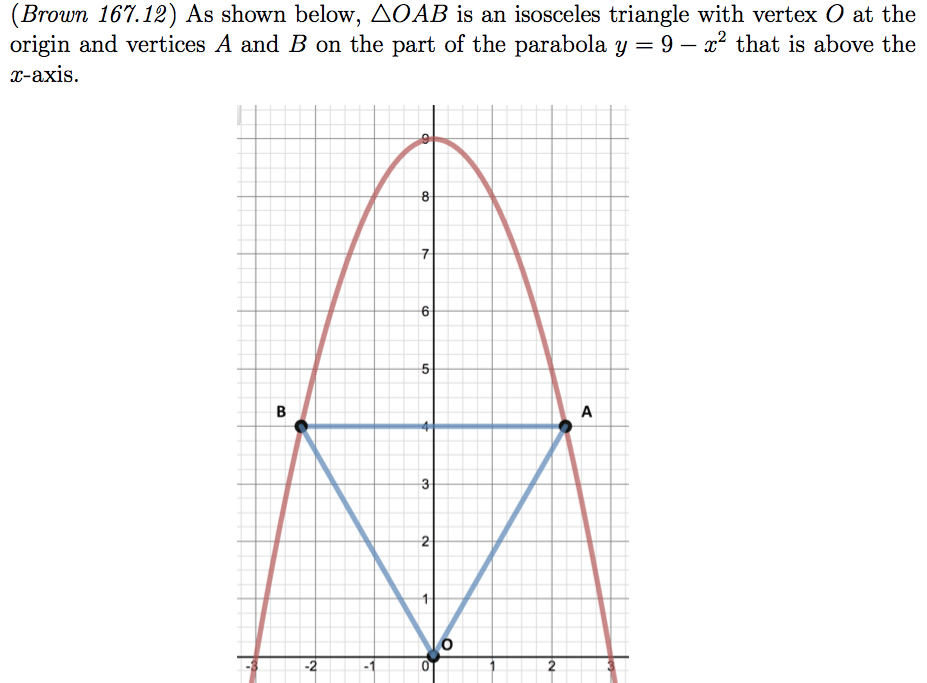
Untitled3

I’ve always been fascinated by these types of problems because they’re easy to understand and make guesses about but often have unexpected solutions. I wanted to use Desmos to bring this problem to life, so I put together a Desmos activity and companion sheet (.docx version) to look at four of these problems.

Students worked in groups, and they while they all had their own screen, they were expected to move together and come to consensus on the best possible shape before moving on. This fostered lively debate among students as they tried different shapes and improved their guesses by manually calculating areas.

For the “isosceles triangle under a parabola” problem shown above, there were a variety of responses, but there was convergence around the optimal triangle (whose vertex in Quadrant I is (\sqrt{3}, 6):

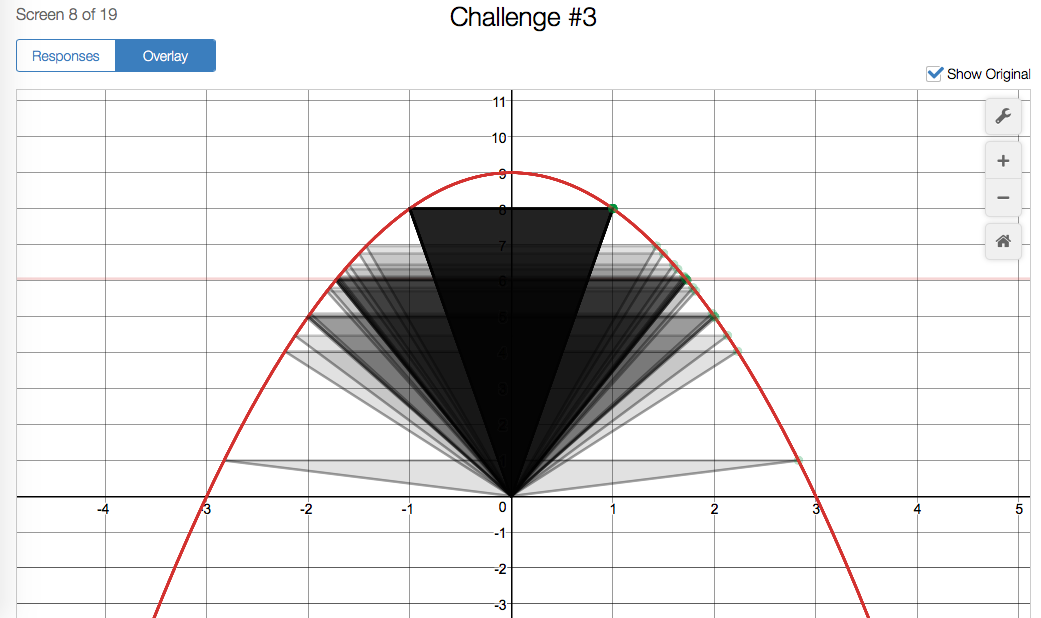
Untitled.png

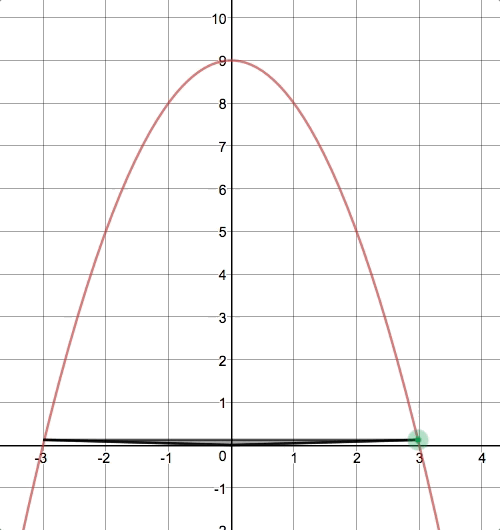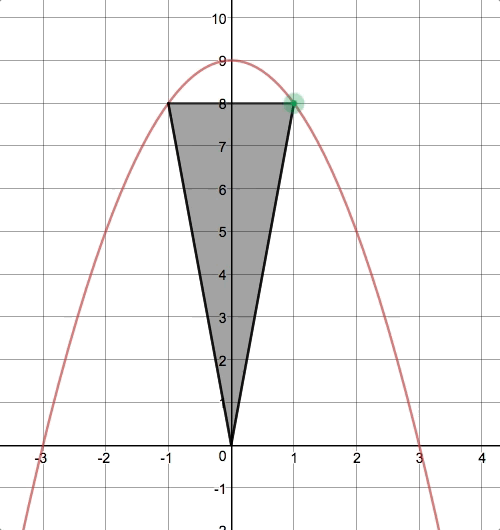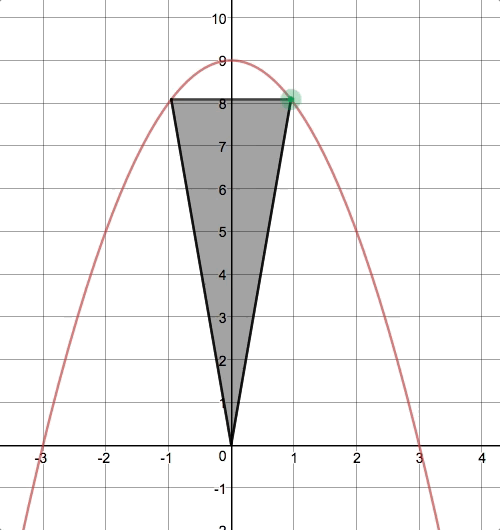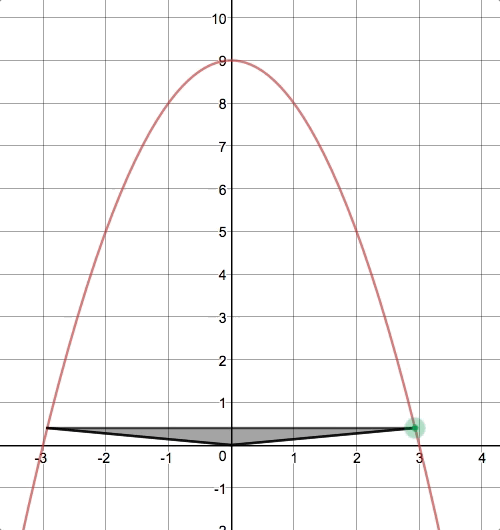
Students were also asked to identify the constraints of their shapes before moving on to the next challenge. After locking in their guesses for each challenge, students had to really dig in to the second challenge (the “rectangle under a parabola” problem). This time, we provided a slider that would calculate the area of the rectangle for them as they changed the x-coordinate of the vertex in Quadrant I:

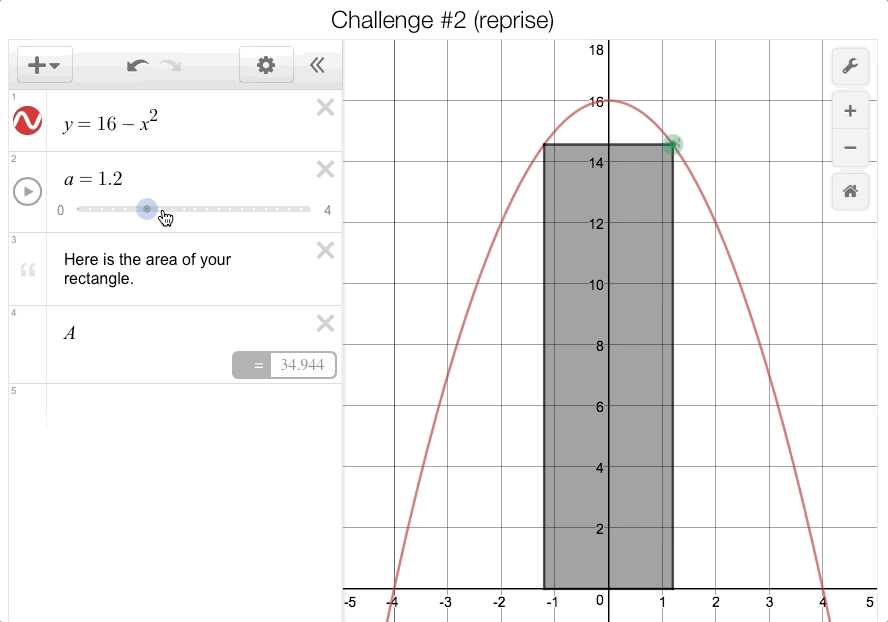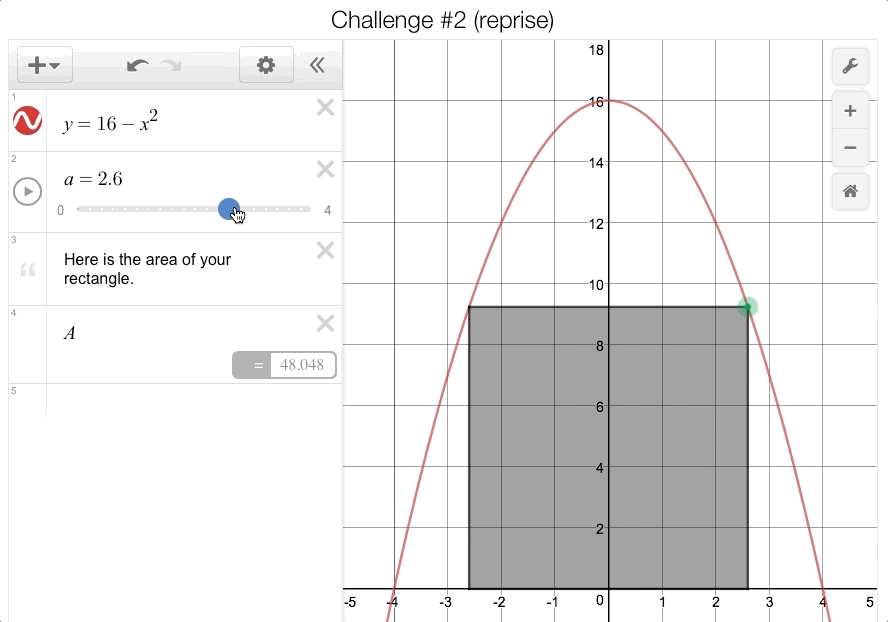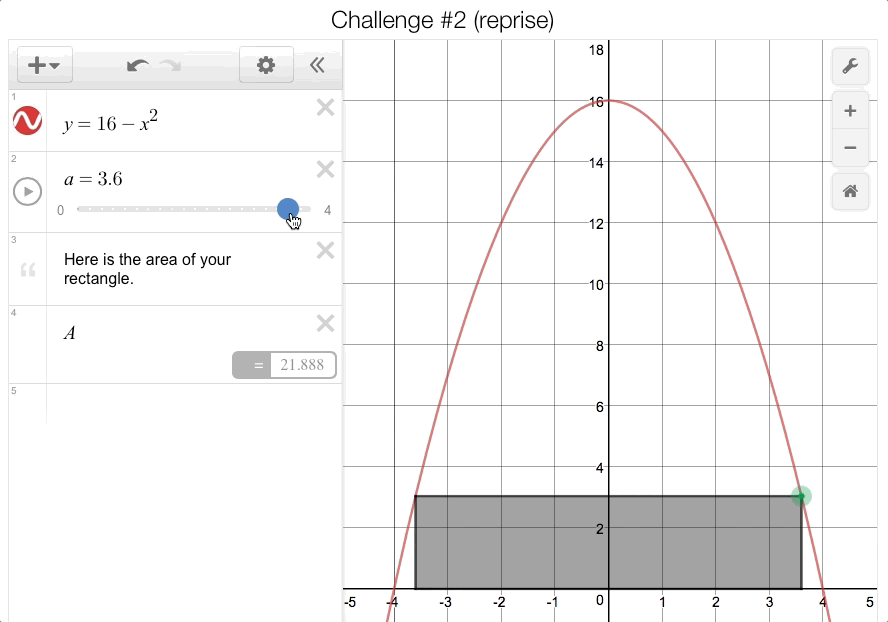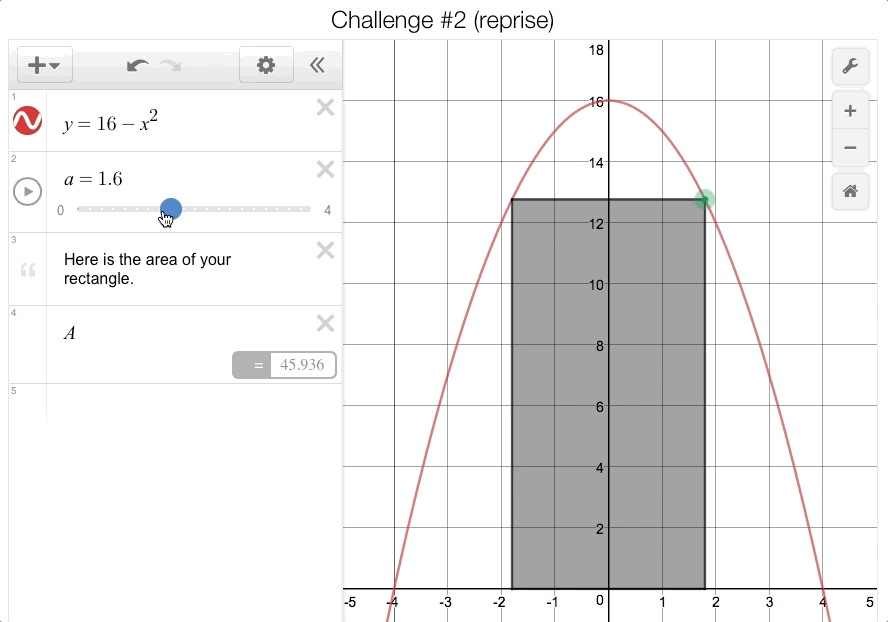
Feb-01-2018 16-47-47

Student were expected to record these data points on the companion sheet to form a sketch of the area function:

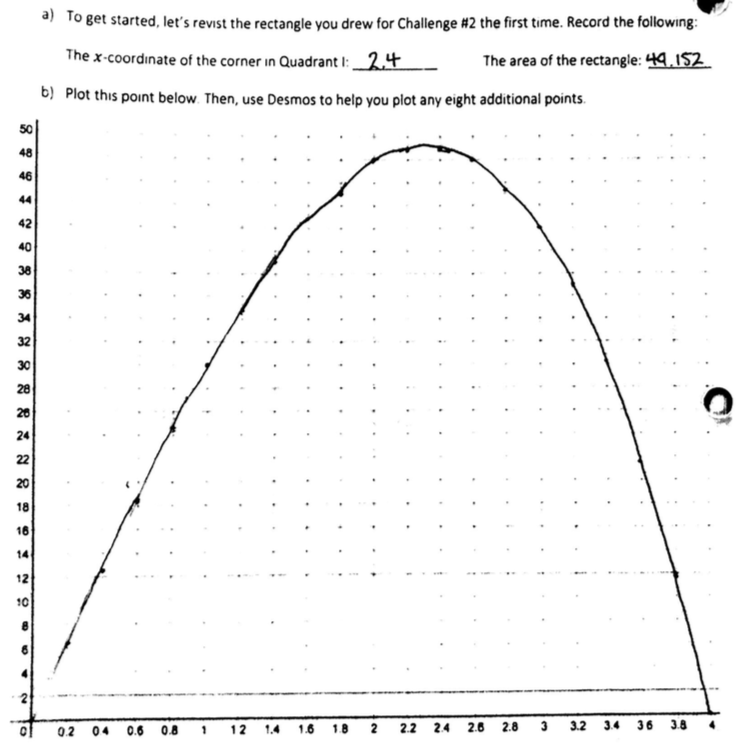
challenge2.png

Many students initially assumed that this area function was going to form a parabola, but after plotting more points, the class decided that it couldn’t be because of the lack of symmetry. But this function has a peak—how could they find it? This is where the calculus kicked in!

After carefully taking the derivative of the area function, setting it to 0, solving, and determining the dimensions of the best possible rectangle, students were able to finally determine which group came the closest with their initial attempt. They were also ready to tackle the remaining challenges on the second part of the companion sheet (.docx).

Before jumping in, I was also able to recognize groups for getting the closest to the best possible shape while also pointing out that they could do even better!

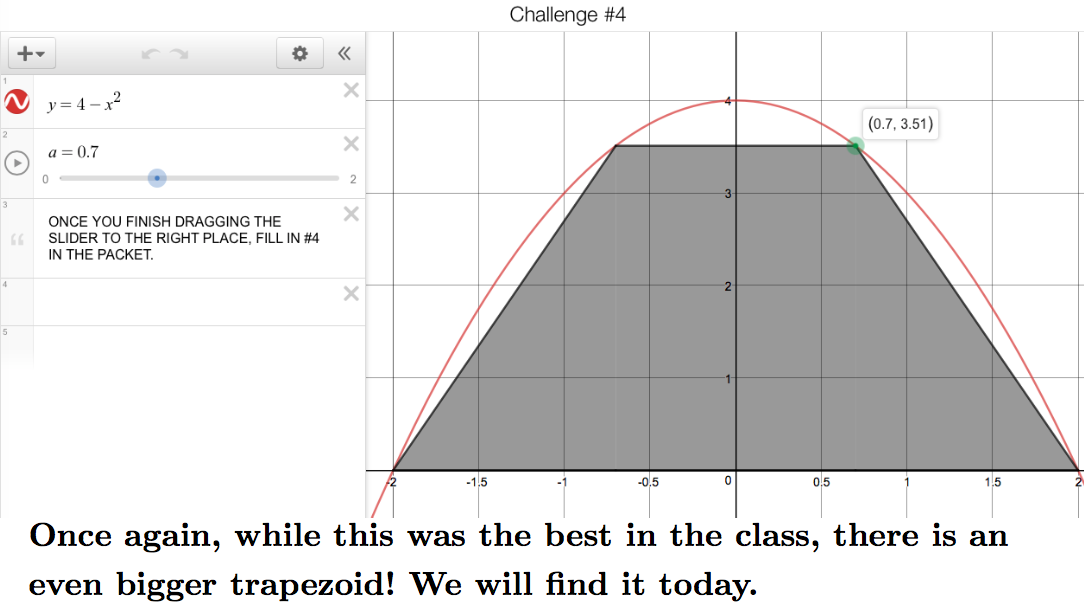
Untitled2.png

All in all, I thought this was a super fun way to kick off the optimization unit while keeping engagement high and providing valuable practice with the non-calculus algebra that can trip students up. Most importantly, calculus was positioned as the aspirin for the headache posted by the Desmos activity.

I would love to see these types of optimization problems become more popular!

Resources:

P.S. See Sam’s post on a lovely lesson he put together called POP! Popcorn Optimization Problem, which is a way more engaging way for students to tackle traditional optimization problems that usually look like this:

original-439030-1.jpg

by Tom James

More on Grading—A Synthesis of Some of my Favorite Thinkers (Part One)

This is part one of a series I’ll be writing on grading.

Guskey, Kashtan, and Reeves

On his blog, Douglas Reeves writes:

I know of few educational issues that are more fraught with emotion than grading. Disputes about grading are rarely polite professional disagreements. Superintendents have been fired, teachers have held candle-light vigils, board seats have been contested, and state legislatures have been angrily engaged over such issues as the use of standards-based grading systems, the elimination of the zero on a 100-point scale, and the opportunities for students to re-submit late or inadequate work.

Miki Kashtan, co-founder of Bay Area Nonviolent Communication, succinctly and insightfully explain  what’s needed to ground intense conversations in cooperation and goodwill:

Focusing on a shared purpose and on solutions that work for everyone brings attention to what a group has in common and what brings them together. This builds trust in the group, and consequently the urge to protect and defend a particular position diminishes.

In On Your Mark (Solution Tree, 2014), Thomas Guskey backs up Kashtan and calls upon the work of Jay McTighe and Grant Wiggins on backward design when he writes, “Method follows purpose.” (p. 15)

Guskey continues to emphasize the importance of beginning with the end in mind when we come together to discuss our craft with other educators:

Reform initiatives that set out to improve grading and reporting procedures must begin with comprehensive discussions about the purpose of grades … (p. 21)

Summary

  • Discussing grading can quickly become prohibitively emotional. (Reeves)
  • Focusing on a shared purpose helps those of us who have already put a stake in the ground to be willing, eager and able to move it. (Kashtan)
  • Before considering the “how” of grading, deeply consider the “why.” (Guskey)

A couple questions on my mind

  1. What practices do you, your department, and/or your institution have in place to facilitate difficult conversations about grading, reporting, and assessment?
  2. To what extent would it be a useful exercise for each department within a school to produce its own purpose statement for grading? (“The purpose of grades within the ___ department at ____ School is …”)

More to come.

by Tom James

Planning for Accelerated Precalculus

This fall, I’ll be teaching a group of very strong students in the highest of three levels of math my school offers. The goal is to give students an intense “Honors Precalculus+” treatment and get them started on calculus (up through the product rule or so) by the end of the school year so that they can jump right into BC Calculus the following fall.

I’m working on developing the standards for the course, and I’m using the model of “performance indicators” and “learning targets” I grew familiar with when I worked at a mastery-based learning school in New Haven. (For background, see the Great Schools Partnership’s document Proficiency-Based Learning Simplified)

I would welcome your thoughts on these learning goals. Do any of them feel too easy? Too difficult? How is the balance? If you had to write an essential question capturing these standards, would would it be?

Finally, here’s some additional background on where I’m coming from.

Source Materials

I’m building this course based on a few sources of problems and materials:

Influential Books

Here are a few books I keep thinking about as I plan this course: