I decided to re-sequence my start-of-the-year activities and to lead with a low-floor, high-ceiling problem in assigned random groups of three or four students.

Here is the problem, which comes from Phillips Exeter Academy’s Math 1 curriculum:

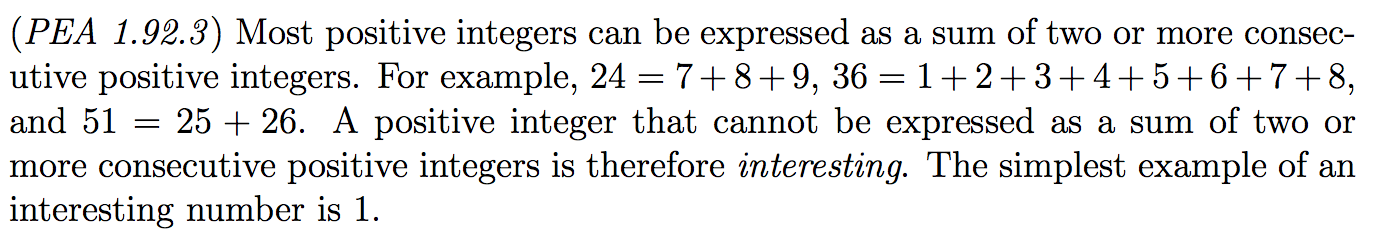
I told the groups to figure out everything they could about this situation with prompts like, “What do you notice about interesting numbers? What do you wonder about them?”

As I watched twelve groups of students explore this problem over three classes, I began to see students latch onto different aspects of this problem. All of these questions and discoveries are inter-related, so I’m writing them down now so that I can map them out in the future.

Questions:

1. Which numbers up through 20 (or so) are interesting?
2. Why are powers of 2 interesting?
3. Are powers of 2 the only interesting numbers?
4. Are there any interesting odd numbers?
5. What happens when I sum any two consecutive positive integers?
6. What happens when I sum any three consecutive positive integers?
7. If n is odd, what happens when I sum any n consecutive positive integers?
8. If n is even, what happens when I sum any n consecutive positive integers?
9. How can I decompose any odd number?
10. How can I decompose any multiple of 3?
11. If n is odd, how can I decompose any multiple of n?
12. How can I decompose any even number?
13. Is there a general algorithm for decomposing any number?
14. How many ways are there to decompose a given number?

Realizations:

1. All powers of 2 are interesting.
2. Only powers of 2 are interesting.
3. No odd numbers are interesting.
4. The sum of two consecutive positive integers is odd.
5. The sum of three consecutive positive integers is a multiple of 3.
6. If n is odd, the sum of n consecutive positive integers is a multiple of n.
7. If n is even, the sum of n consecutive positive integers is n/2 more than a multiple of n.
8. There is an algorithm for decomposing even numbers.
9. There is exactly one way to decompose a prime number greater than 2.
10. The powers of 2 are exactly the whole numbers without odd factors.

There was a split between groups that started by trying to answer (the very natural) question #1 (and thus getting to realizations #1 and #2) and those that started by generating and then trying to answer questions #5 and 6 (and thus getting to realizations #4 and #5). There was also one group in one class that decided to explore the sum of the first n consecutive integers (i.e., they wanted to know about the triangular numbers).

I think I will definitely use this problem again, with perhaps a bit more structure and guided mini-explorations along the way as groups arrive at various questions and realizations. It would probably be worth making a checklist for each group to help keep me organized as I keep tabs on each group’s progress.

Related:

• https://mathblag.wordpress.com/2011/11/13/sums-of-consecutive-integers/
• https://nrich.maths.org/507
• https://blogs.adelaide.edu.au/maths-learning/2015/07/28/the-sausage-stacking-theorem/