My love of the outdoors really took off in the summer of 2021, so it was a joy and coming-full-circle moment to co-guide a wilderness expedition in the summer of 2023 for a group of teenagers in the Four Corners region near southwest Colorado. My friend Patrick, who’s the Assistant Director at Camp Pemi, put together a great blog post about the trip!
Here’s a full trip report I wrote if you’re curious about what it was like day by day.
I’ve been thinking about the extent to which there is tension between the principles of Universal Design for Learning and progressive, inquiry-based, student-centered math teaching.
I’ve done a lot of math teaching in independent schools that falls within the rightmost section, and some in the sweet spot in the middle. Within the public and charter school system, the challenge has been more about moving from the splash of inaccessible, traditional math teaching into universally designed (but still fairly traditional) teaching.
For a bit of background, UDL is an educational framework that began in 1984 which calls for multiple means of engagement, representation, and action/expression to ensure access for all learners by removing barriers to learning. You may have seen this visual metaphor:
UDL is a rightfully ambitious framework which in practice is aspirational rather than fully realized in any particular lesson, unit, or course. When it comes to access to mathematics, the challenge is in the implementation details of any curriculum or pedagogical approach.
When I think about implementations of a progressive math teaching philosophy, approaches such as Exeter Math (problem sets) and Building Thinking Classrooms come to mind. I’ve used aspects of both of these over the years. Both of them hold student collaboration as a central course goal. They are both opinionated about how students should work (together, often at the board) and that students should learn by solving problems and generalizing from there.
I’ve been wondering lately about the extent to which these progressive, inquiry-based math approaches can be inaccessible to some students based on their learning needs. And if so, are these barriers that can be removed, or are they intrinsic to the particular approach?
I happen to be a huge fan of Exeter math. I love the spiraled problem sets, the fact that students are expected to own the cognitive lift, and the way the curriculum emphasizes connection, sense-making, and novel problem solving. At the same time, I also recognize that it’s not an approach that could be widely adopted at schools across the country. There are practical barriers in terms of the time commitment required outside of class, lack of board space and large class size in many places, and limited opportunities for differentiation. This makes me wonder about what a universally designed, problem-based approach would look like.
To meet the requirements of UDL, it seems the things we can be opinionated about as teachers and curriculum designers have to be limited. For example, we can still insist that students do most of the talking and thinking within the classroom. But we probably have to let get the requirement that students work in groups most of the time since this infringes on student choice. (To me, there is a balancing act to navigate between UDL Checkpoint 8.3 about collaboration and community and UDL Checkpoint 7.1 about individual choice and autonomy.) That’s a painful concession for me to consider because of how strongly I believe in the value of collaboration in math class.
I’m sure many educators have found ways over the years to take these progressive math approaches and make them accessible to as many students as possible. I wonder if these are some of the both/and beliefs they embody:
My school’s math department has been working hard to articulate a vision for an anti-racist math program and to take action to realize that vision. I’m grateful to our talented communications department for highlighting this ongoing work!
As a study of quantity, structure, space, and change, mathematics might not be top of mind as a discipline in need of an anti-racist lens. However, from the origin of the number system we use today to the mathematicians who are studied and revered, elements of white-washing and exclusion can be found throughout the field.
Packer’s mathematics department has been exploring ways to address race and equity in both its curriculum and its teaching practices. This is a reflection of the teachers’ own interests, as well as a response to Upper School students’ call this past summer for the re-evaluation of curriculum throughout the division.
“There’s a hunger for how math can be used to make the world a more equitable space, how it can be used to understand racism and other dynamics of oppression and how it can be used…as a tool for social justice,” said Interim Upper School Math Department Head Tom James.
Last spring, the math department held an anti-racist math teaching forum, where they identified issues of racial inequity and pulled together a collection of anti-racist resources. The group has been working to articulate a vision for what anti-bias and anti-racism looks like in their department. While the group has addressed gender bias in the past, Tom said, “it’s important to focus anti-bias work on race specifically because that’s an area of growth for us and something that needs to be named explicitly.”
The teachers’ work, coupled with the feedback shared by the student-led Change Committee, has brought noticeable changes to what is taught in Upper School math classes and how. The department employs a “journey partners” model to support educators in this work. In pairs or trios, math teachers work together to develop and implement anti-racist curriculum changes in their respective classes. Through regular check-ins, the partners serve as sounding boards for new ideas and as accountability buddies in the process of unlearning racism and bias. …
One noteworthy focus is the way in which teachers are attempting to shape classroom culture. While collaboration is common in other disciplines, Tom said students sometimes approach math with a strong focus on personal rather than collective understanding—a mindset that is prevalent in dominant culture. …
“A lot of teachers in our department are very deliberate about emphasizing really strong collaboration, teaching those skills explicitly,” said Tom. “[They’re] sending the message very directly that [math] class is not just about you being in it for yourself and your own understanding, but actually about building collective understanding.” …
In Tom’s Advanced Algebra II and AT Symmetry and Transformations courses, he is working to humanize mathematics by having students read stories about the professional journeys of mathematicians across identifiers. “It’s important to us that we’re not tokenizing mathematicians of color, so we’ve looked at female mathematicians, LBGTQ+ mathematicians, mathematicians of color, of a number of different backgrounds,” said Tom. Classroom discussions explore the positive and negative forces these professionals have faced and how those same forces show up in Packer’s classrooms.
These examples represent just some of the immediate ways in which the mathematics department has answered the call to become anti-racist. On-going efforts will include additional shaping of the curriculum as well as further exploration about how math is taught, how work is graded, and how to achieve proportional representation across course levels. The goal of this work is to create an inclusive and supportive learning environment so that all students will be equally engaged in the study of mathematics.
“We really want students to understand that acquiring mathematical knowledge and expertise is in itself an act of personal and collective liberation,” said Tom. “These are the tools you need in order to both understand and come to terms with [the idea that] society is not the way we want it to be and to be able to make a plan toward building a more equitable and just society.”
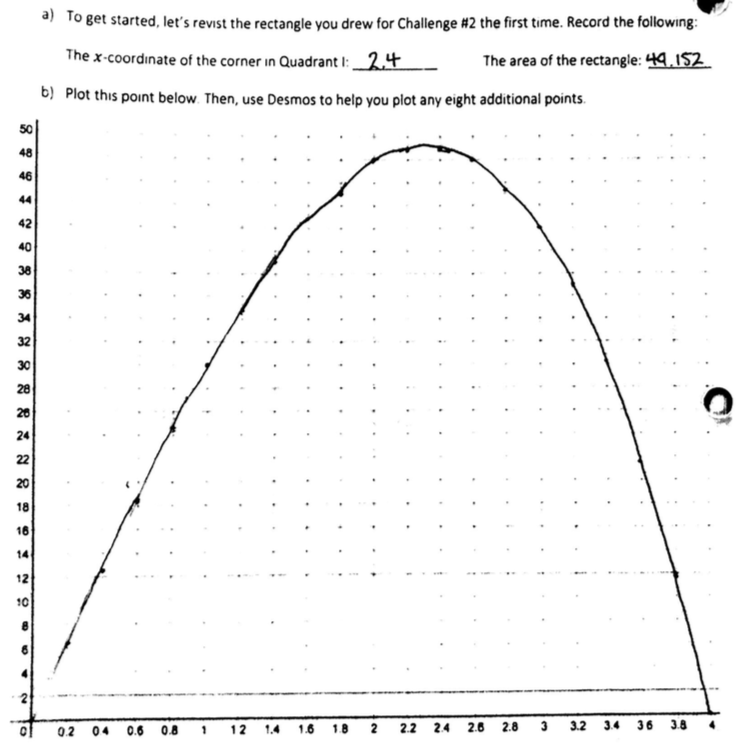
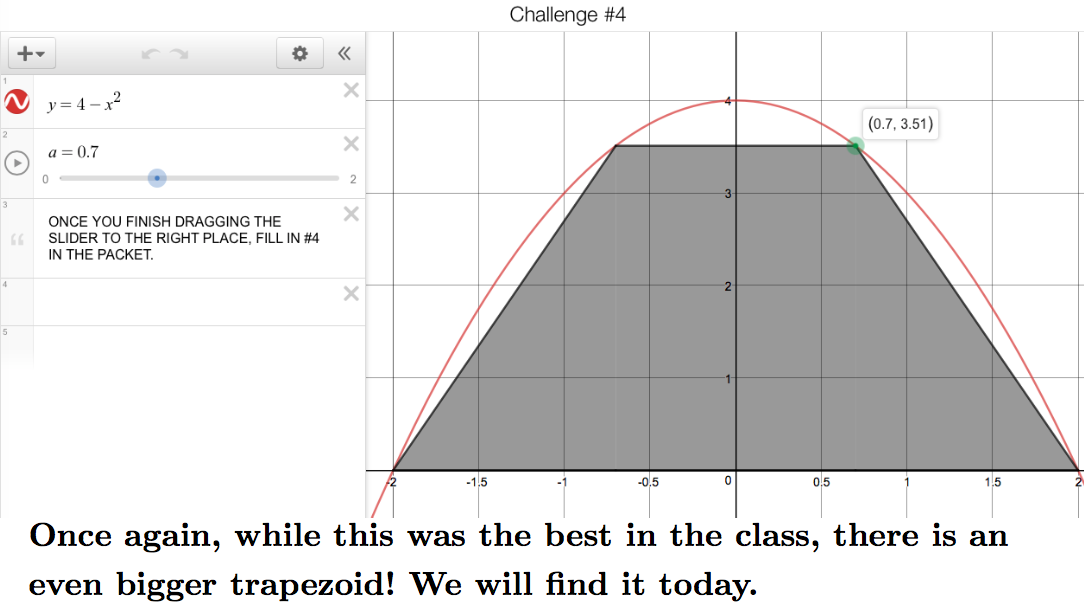
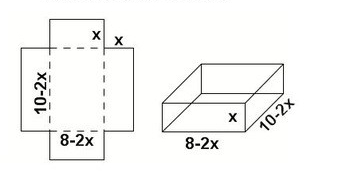
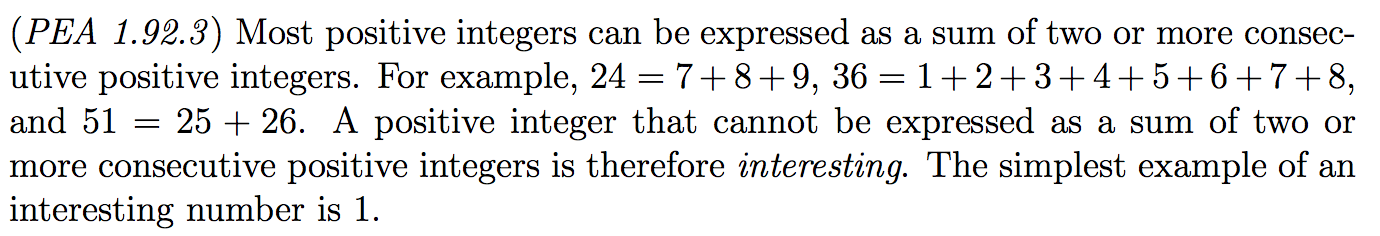(I wrote most of this post before the school year started but didn’t get around to publishing—using the end of winter break to finish it off!)
I’ve been teaching pretty much non-stop since I started in 2012. Every summer I’ve been an instructor at a couple different summer academic programs (a.k.a. nerd camps). But this summer, I took a break from teaching to work on a master’s program in educational leadership. This meant taking five classes in six weeks:
Beyond Winning. The chapters specific to lawyering can be skipped.
Source: Mnookin, Robert H. Beyond Winning Negotiating to Create Value in Deals and Disputes. Harvard: Harvard University Press, 2004.
Difficult Conversations. This is worth rereading a chapter or two every month.
Source: Stone, Douglas, Bruce Patton, and Sheila Heen. Difficult Conversations: How to Discuss What Matters Most. Yuan Liou Publishing, 2014.
Epistemic Injustice: Power and the Ethics of Knowing. The concept of “testimonial injustice” is useful for naming systems in which marginalized individuals’ voices are met with doubt and disbelief. The first chapter of Fricker’s book very carefully builds up definitions along with examples and non-examples. I’d like to read the rest of this book where she develops the idea of testimonial justice.
Source: Fricker, M. (2011). Epistemic injustice: Power and the ethics of knowing. Oxford: Oxford University Press.
Caring: A Feminine Approach to Ethics & Moral Education. In the first chapter of this book (“Why Care About Caring?”), Noddings develops the concept of “care ethics.” Whenever I get bogged down in the details of math pedagogy, this chapter will be an important resource for humanizing the process of education and our students’ needs as human beings.
Source: Noddings, N. (2003). Caring: A feminine approach to ethics & moral education. Berkeley: University of California Press.
Democracy and Education. In the chapter “Education as Growth,” Dewey names a mechanism through which much of the deficit thinking about children and adolescents arises. When we think about students as unfinished adults, we necessarily close ourselves off to the powers and strengths unique to young people. This chapter is worth rereading every year.
Source: Dewey, J., & Boydston, J. A. (2008). The middle works, 1899–1924. Carbondale: Southern Ill. Univ. Press.
Educator Competencies for Personalized, Learner-Centered Teaching. This resource enumerates and unpacks the skills, understandings, and dispositions teachers need to enact student-centered practices. I’ve previously focused on making sense of the instructional and cognitive competencies, and this report also dives into the interpersonal and intrapersonal dimensions of student-centered teaching. I could see myself using this to ground myself as I analyze the competencies that are present in myself and the educators I’m working with.
Source: Jobs for the Future & the Council of Chief State School Officers. 2015. Educator Competencies for Personalized, Learner-Centered Teaching. Boston, MA: Jobs for the Future.
Leadership for Increasingly Diverse Schools. An equity audit can be used to identify and address issues concerning proportional representation in various areas of the school. The suggested timeline for accomplishing goals is about three years, and it’s crucial to link these goals to student learning. This tool provides a clear structure for meeting a particular type of school-based inequity head-on.
Source: Theoharis, George, and Martin K. Scanlan. Leadership for Increasingly Diverse Schools. Routledge, 2015.
Organizational Culture and Leadership. The opening chapters from this resource pushed my understanding of organizational culture forward by laying out three levels of culture. I particularly appreciated the explanatory power of invisible but deeply influential underlying assumptions when we encounter structures and behaviors that don’t align with our publicly stated beliefs. I could see myself appealing to the lily pond metaphor to explain this idea to others who are invested in change. I’d like to read more out of this.
Source: Schein, Edgar H. Organizational Culture and Leadership. 5th ed., Wiley, 2017.
Dilemmas of Educational Ethics: Cases and Commentaries. Our ethics professor suggested we read this. Reading and thinking through case studies was one of my favorite activities of the class, so I’m looking forward to reading this.
Source: Levinson, Meira, and Jacob Fay. Dilemmas of Educational Ethics: Cases and Commentaries. Cambridge, MA: Harvard Education Press, 2016.
Visible random groupings.
Retrieval practice.
Spaced practice.
Interleaving.
Connecting to prior knowledge.
Coaching. By offering help to my advisees in a non-directive way, I can honor their autonomy and ability to solve their own problems. There’s a toolkit I can use that focuses on the now and the future and spends more time on the values, wants, passions, and motivations of the person I’m working with. This is more effective than jumping right into the logical and logistical domains. I can also practice asking more “what” than “why” questions to keep the focus on coaching the person, not the problem.
Sharing hopes/fears anonymously.
Listening walks. Slow down in the hallways.
Teaching metacognitition explicitly.
Teaching executive functioning skills explicitly. For example, have everyone write on an index card the “movie script” of how they did their homework. Where were they physically? What time was it? Where was their phone? What resources did they use? Collect, shuffle, and redistribute the cards. In groups, compare the approaches. Share out the ones that sounded most effective.
In the somewhat rushed lead-up to our unit test on logarithms in my Advanced Algebra II class, I realized I was asking students to study from an enormous corpus of practice material I’d provided. I could tell that this was overwhelming, so I got the idea to give the test to my students in advance.
Not the full test—just a redacted version:
I had dropped a hard copy in one student’s open backpack during a break, and then I made a big show of asking him to pull out the paper marked “top secret.” Then I was all, “ohmygoodness what’s that?!” and “Did I accidentally post a copy of the test to Google Classroom?” My students were thrilled. (I did make it clear that this was a one-time thing!)
Even though I had already provided a list of learning targets, I had two main goals by “leaking” the test itself:
This was a spur-of-the-moment idea, but definitely one I would use again under the right circumstances!
I teach in a progressive math department committed to inquiry-based learning, and I’ve been working on sharpening how I talk about why I believe in this approach.
A conversation will often start when I hear a student or a parent say one of these:
It’s hard to imagine what an inquiry-based math class looks like if you’ve never been in one. I suspect that if you’re a parent and your child is experiencing math-related stress or frustration, there are a few reasons you might order if this way of learning is best for your child. These are some of the images you might conjure up:
When I think about an inquiry-based math class looks like, I see something very different:
Ultimately, every parent comes to these conversations about math education with the goal of seeing their child successful and happy. Keeping this in mind is critical for addressing their concerns.
Over at the IBL Blog, Stan Yoshinobu writes about the feelings can arise when students haven’t bought into the value of productive struggle:
Mindsets are at the core causes student buy-in issues. When students don’t buy it, it’s often because they don’t like being stuck or that being stuck implies there is something wrong with the problem, them, or the teacher or all of the above and more.
I was digging more into the IBL Blog and discovered this lovely metaphor of “I don’t learn this way” as the tip of the iceberg:
This imagery reminds us to look beneath the surface to find the source of resistance to inquiry-based learning. Only then can I speak to my beliefs and vision for my students.
I believe in inquiry-based learning because I think students learn math best when…
I’ll conclude with some prose from Joshua Bowman, who recently shared a preface he wrote to an IBL course. Here’s an excerpt:
… [T]he success of the class will depend on the pursuit of both individual excellence and collective achievement. Like a musician in an orchestra, you should bring your best work and be prepared to blend it with others’ contributions.
… Mistakes are inevitable, and they should not be an obstacle to further progress. It’s normal to struggle and be confused as you work through new material. Accepting that means you can keep working even while feeling stuck, until you overcome and reach even greater accomplishments.
This is a follow-up post to my first day math problem from last year.
I’ve only posted once in a while over the past few years, but I’m very glad I spent the time last year to write about how my first day math problem went. After re-reading my post from last year, I was able to rapidly load the problem and how it went back into my memory, and I decided to make some of the changes I had written about.
Here’s the updated version of the problem, which adds scaffolding and will hopefully keep groups moving along who aren’t as comfortable with this type of open-ended exploration.
And here’s the checklist I’m going to use to keep myself organized as I walk around and monitor each group’s progress. (This idea comes from 5 Practices for Orchestrating Productive Mathematics Discussions by by Margaret S. Smith and Mary Kay Stein.)
Feel free to pass along any feedback or take this a step further!
Resources:
This is my contribution to The Virtual Conference of Mathematical Flavors.
In order to figure out what flavor of math I’ve been serving up in my classrooms over the past six years, I’m going to take a stab at Sam Shah’s idea of working backwards from what students have written about their experiences in my math classes. (Spoiler alert: the answer is apparently pomegranate; who knew?!) Of course, not all of my students have had transformative experiences and others have straight up had a bad time. But right now, I’m going to focus on the students who have been positively impacted in order to articulate what the best implementation of my ideals has felt like.
But to be honest, it feels way scarier to share the positive things students have written about me over the years than anything critical. When I was younger, I used to brag and show off; I thought that if people knew about all the things I was good at, they would have to like me. Once I figured out that this is not how relationships work, the pendulum swung hard in the other direction for me. I grew increasingly uncomfortable accepting compliments and I minimized my achievements, working to avoid even the appearance of self-promotion. It’s an ongoing struggle to get right-sized, but lately I’ve begun to internalize the idea that being excessively diminutive is its own barrier to connection.
So with that confession out in the open, here are some of my favorite reflections students have written. (The title of this post comes from one of these!)
I would like to thank you for all your effort and enthusiasm you've brought everyday for the last nine months. Your passion for math often even overcomes my languidness at the day's end. Many teachers do not really care for their subject, and in those classes I wonder why I should care. However, you clearly love math, and while I may not share the same caliber of adoration for numbers and their wacky properties, you keep my interest in math alive. Additionally, I recognize and appreciate all the organization and extra work you do to help us succeed. The online problem sets, solutions, carefully crafted test solutions, and progress sheets are but some of the many things which have helped me study harder and study better. You are the most passionate teacher I have ever had, and for that I cannot thank you enough.
Thank you so much for being an amazing, dedicated, and exciting teacher! I'd like to amend my "math is like a ____" from earlier this year (thanks to this class and you). Math is like a pomegranate—intimidating, and kinda scary looking at first, but also incredibly fascinating and vibrant.
I loved Precalc and because of your teaching style and love for math, my love for math grew as well. Honestly sometimes I'll be lying awake thinking about something we learned in class and tears will come to my eyes because math is so beautiful. Thank you for teaching me that.
This was by far my favorite math class ever, and math is already my favorite academic subject. Like I told you in class, your enthusiasm is nothing like anything I've seen in any other teacher I've had, and it was always a pleasure to learn from you.
Your enthusiasm and patience is honestly inspiring. You make me want to succeed in math, and the units on imaginary numbers and limits have made me excited about finding interesting and creative solutions to problems. This has made me seriously consider doing something math based in college or even as a career.
I honestly think you have been one of the best math teachers I have had because I feel like the class was fun and you are so enthusiastic about the concepts that you teach us that I was excited to understand things (like De Moivre's theorem or binomial expansion) too. I felt like I really understood the expectations of the class and that I wanted to try my best; I also think you are very approachable and I felt comfortable asking for help in or outside of class. I also think you had a really good balance between letting us present problems to each other and stepping in to make corrections or add information, and you did it without making me feel bad for missing something or making a mistake.
I think this year has really been a turning point in my academic career, and I owe a lot of that to your teaching. Leaving this class, I am much more confident in my abilities and I have learned to take a lot of pride in my work, not to mention A LOT about math.
You have grown my love for this subject and blown my mind of multiple occasions and your everlasting enthusiasm for the subject fuels my own. I genuinely feel your love for math, wresting, cross country, and ever more things and it honestly makes me so happy. Your passion for the things you love inspires me to put all my heart into the activites that can challenge me but also bring me joy.
A few years ago, I started asking students to write advice to next year’s students. And when I remember, I make sure to share this advice once the new group arrives. Here are some examples of what my students have written.
Be ready to push yourself and put your mathematical skills to the test as some, if not most of the new material, will be more abstract and quite difficult. If ever you are stuck on anything, do not hesitate to ask for assistance from your fellow students and of course, your teacher. This course isn't defined just by its challenge, however. The new concepts you will learn are some of the coolest and fascinating topics in the entire world of math. I encourage you to let yourself truly absorb and enjoy what it is you will be learning, and from there you will find immense satisfaction in discovering the new mathematical ideas and techniques found in this overarching course.
I know; it doesn't feel like you're quite old enough to use the word "calculus" when referring to your classes. Actually, it feels a little overwhelming. Some of you can't help but think that math is really *not* your forte, or maybe you're thinking "I'm going to crush it". Maybe you're just here for the giggles. I can assure you that this class will be challenging and frustrating, will involve broken pencils and maybe a couple of tears. It will all be worth it. Because no matter what kind of math student, no matter how prepared you feel, at some point, you will have an "a-ha" moment. And all of the numbers, limits, combinatorics, whatever it is - it will make sense. And that will be the best moment of the year.
Get excited because this year of math with blow your mind. There might be some hardships, but it is worth it in the end. Be open to new methods of learning and approaching problems from different angles. Always trust your instincts and when you come to a complicated problem try to think of it as a simpler problems first.
You’ll actually perform a lot better on tests when you’re at a table where you feel comfortable asking questions and where other people feel comfortable asking you questions.
This part is really important: offer guidance. Some people are often afraid of seeking help when they don’t understand something because they may think that you’ll judge them or think they’re stupid. If you sense someone struggling, ask them if they understand the problem. If not, try to walk them through it, and please don’t get frustrated. It sucks to be on the other end of that frustration, especially when you didn’t seek it out yourself. The goal of this guidance isn’t to prove yourself or your own abilities; it’s to help your classmate understand a topic that they’re struggling with.
This course will be very challenging for you. The homework will take genuine effort and time and there is no way you can BS your way through a Mr. James test. That said, it will also push you to be a more self-reliant math student. You will gain confidence in your ability and leave the course ready and excited for advanced pre calc.
Not to scare you, but math this year will be challenging. You aren’t going to understand everything right away, or get the perfect score on every test, or always know the right answer. You’re going to need to ask for help, and you’re going to need to learn to be okay with that. While this class may not be easy, though, it will be useful in learning about yourself both as a math student and as a student in general.
It is often tempting to move through the academic part of school stuck in a rut of individualism. That is not to say that it isn’t beneficial to be independent at times, but just that sometimes you will struggle and will need to rely on others, and that that’s okay. Conversely, though, sometimes others will need to rely on you, and offering yourself as a resource will almost always strengthen your own understanding of the material. I know that sounds cheesy, but I genuinely believe that some of your greatest lightbulb moments, mathematical and otherwise, will arise when working through problems with others. Being the helper and being the helped don’t need to be mutually exclusive.
Reading these, some of the core beliefs I bring to my teaching are apparent to students in different courses and at different schools. I hope that my students internalize them as well:
As a final thought, it feels liberating to put this out there in a less formal way than I’ve articulated aspects of my educational philosophy in the past. For comparison, this is what I’ve used in previous job searches, and almost all of it was composed in 2014, before any of the student reflections above were written.
I still stand by everything in this document, but I really appreciate the type of unencumbered sharing Sam’s framing of the prompt for this virtual conference has facilitated. In other words, asking “What mathematical flavor are your serving up?” rather than “What’s your theory of mathematics education?” seems more likely to inspire folks to share a healthy multiplicity of approaches instead of competing formal philosophies. And, it gives us an opportunity to celebrate our wins instead of worrying about all of the things we’re not doing.
I’ve had the pleasure of teaching standard-level calculus with Sam Shah this school year, and recently we’ve been working with the students on optimization. Rather than starting with the canonical calculus optimization problems, we decided to jump in with maximizing the area of various shapes under curves:
I think I first saw a problem like this in a textbook called Advanced Mathematics by Richard G. Brown (page 167, #12):
I’ve always been fascinated by these types of problems because they’re easy to understand and make guesses about but often have unexpected solutions. I wanted to use Desmos to bring this problem to life, so I put together a Desmos activity and companion sheet (.docx version) to look at four of these problems.
Students worked in groups, and they while they all had their own screen, they were expected to move together and come to consensus on the best possible shape before moving on. This fostered lively debate among students as they tried different shapes and improved their guesses by manually calculating areas.
For the “isosceles triangle under a parabola” problem shown above, there were a variety of responses, but there was convergence around the optimal triangle (whose vertex in Quadrant I is 
Students were also asked to identify the constraints of their shapes before moving on to the next challenge. After locking in their guesses for each challenge, students had to really dig in to the second challenge (the “rectangle under a parabola” problem). This time, we provided a slider that would calculate the area of the rectangle for them as they changed the
Student were expected to record these data points on the companion sheet to form a sketch of the area function:
Many students initially assumed that this area function was going to form a parabola, but after plotting more points, the class decided that it couldn’t be because of the lack of symmetry. But this function has a peak—how could they find it? This is where the calculus kicked in!
After carefully taking the derivative of the area function, setting it to 0, solving, and determining the dimensions of the best possible rectangle, students were able to finally determine which group came the closest with their initial attempt. They were also ready to tackle the remaining challenges on the second part of the companion sheet (.docx).
Before jumping in, I was also able to recognize groups for getting the closest to the best possible shape while also pointing out that they could do even better!
All in all, I thought this was a super fun way to kick off the optimization unit while keeping engagement high and providing valuable practice with the non-calculus algebra that can trip students up. Most importantly, calculus was positioned as the aspirin for the headache posted by the Desmos activity.
I would love to see these types of optimization problems become more popular!
Resources:
P.S. See Sam’s post on a lovely lesson he put together called POP! Popcorn Optimization Problem, which is a way more engaging way for students to tackle traditional optimization problems that usually look like this:
I decided to re-sequence my start-of-the-year activities and to lead with a low-floor, high-ceiling problem in assigned random groups of three or four students.
Here is the problem, which comes from Phillips Exeter Academy’s Math 1 curriculum:
I told the groups to figure out everything they could about this situation with prompts like, “What do you notice about interesting numbers? What do you wonder about them?”
As I watched twelve groups of students explore this problem over three classes, I began to see students latch onto different aspects of this problem. All of these questions and discoveries are inter-related, so I’m writing them down now so that I can map them out in the future.
Questions:
Realizations:
There was a split between groups that started by trying to answer (the very natural) question #1 (and thus getting to realizations #1 and #2) and those that started by generating and then trying to answer questions #5 and 6 (and thus getting to realizations #4 and #5). There was also one group in one class that decided to explore the sum of the first n consecutive integers (i.e., they wanted to know about the triangular numbers).
I think I will definitely use this problem again, with perhaps a bit more structure and guided mini-explorations along the way as groups arrive at various questions and realizations. It would probably be worth making a checklist for each group to help keep me organized as I keep tabs on each group’s progress.
Related: